Outcome Probability for One Handed Solitaire

Back in 1994 my circle of high school friends spent a lot of time sitting around talking (there were no cell phones) and for about a week we were all playing one handed solitaire. In suburban St. Louis we called it idiot's delight solitaire (which turns out to be an entirely different game), because there is absolutely no human input after the shuffle. As soon as you've started playing it's already determined whether you've won -- you just spend five minutes learning if you did.

Naturally we wondered how likely our very rare wins were, and being a computer nerd back then too I wrote a Pascal(!) program to simulate the game and arrived at the conclusion you win one in every 142 games.

Now thirty years later I've taught the game to the eleven year old in our home, who is just game back from a phone-free summer camp with a deck of cards and dubious shuffling skills.

My old Pascal is lost to bitrot, but the game as python, using a sort of janky off the shelf deck_of_cards module is trivial:

def play():
    deck = deck_of_cards.DeckOfCards()
    hand = []

    while not deck._deck_empty():
        hand.append(deck.give_random_card())

        while len(hand) > 3:
            if hand[-1].suit == hand[-4].suit:
                del hand[-3:-1]
            elif hand[-1].rank == hand[-4].rank:
                del hand[-4:]
            else:
                break
    return len(hand)

On the 486 I was running at the time I recall getting ten thousand or so runs over many days. On a tiny Linode in the modern era I got 50 million runs in 15ish hours.

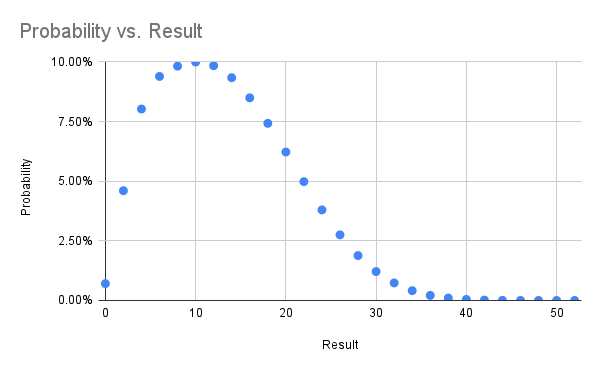
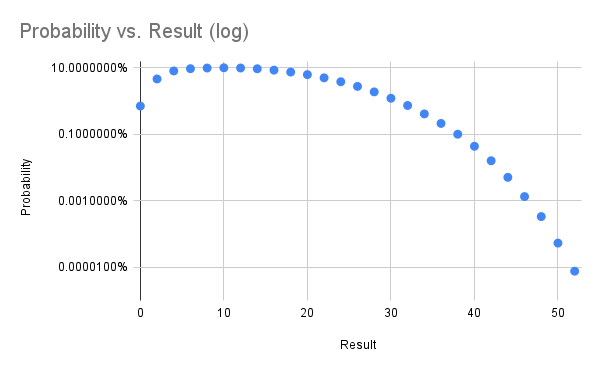
I've gathered the results in a spreadsheet and included some probability graphs below. In trying to find the real name of this game I came across a previous analysis from 2014 which comes to the same overall probability. That blog post is now down (hence the archive.org links) with ominous messages telling folks the author is definitely no longer thinking about this game.